Les opérateurs logiques

Le processeur d’un ordinateur est composé de transistors qui sont des semi-conducteurs. Ils ont la particularité de laisser passer ou non le courant électrique.

En les associant, ils vont constituer des portes logiques qui modifient les courants électriques et donc les valeurs des bits \(0\) et \(1\).

Exemple

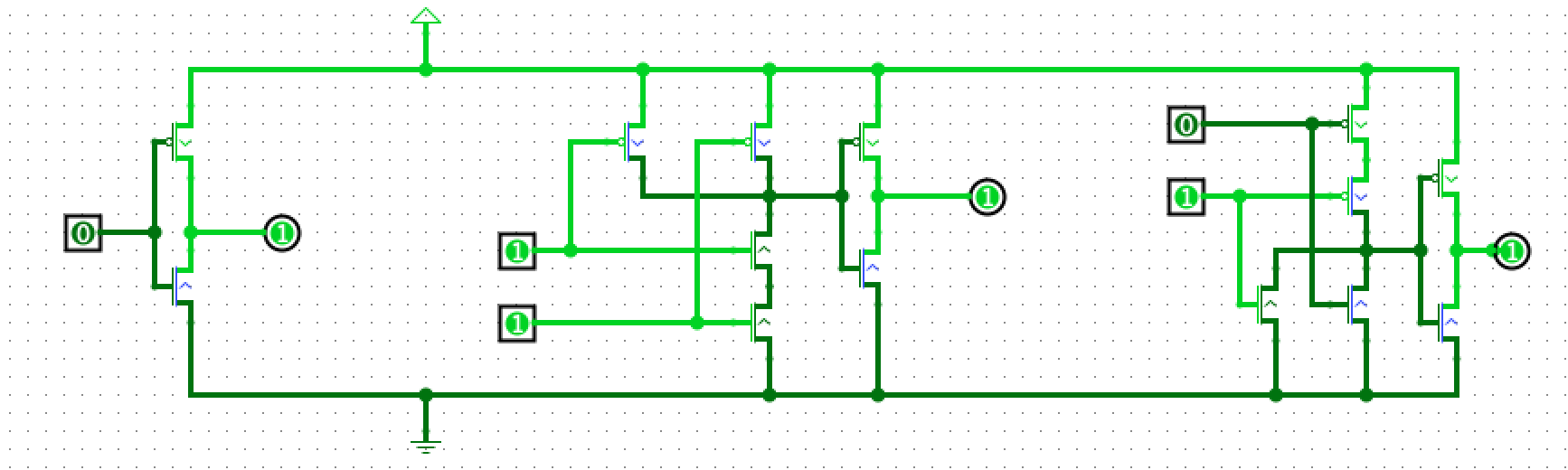
Sur la figure ci-dessous réalisée avec l’application java logissim, on a reproduit avec des transistors:

• à gauche la porte logique not;

• au centre la porte logique et;

• à droite la porte logique ou.

La porte logique NOT

La porte NOT a un seul bit d’entrée et un seul bit de sortie.

• Si le bit d’entrée vaut \(1\), alors il vaut \(0\) en sortie.

• Si le bit d’entrée vaut \(0\), alors il vaut \(1\) en sortie.

On donne les symbolisations de la porte NOT et la table logique:

La porte logique ET

La porte ET a 2 bits en entrée et un seul bit de sortie.

• Si les 2 bits d’entrée valent \(1\), alors le bit de sortie vaut \(1\).

• Si un bit d’entrée ou les 2 valent \(0\), alors le bit de sortie vaut \(0\).

On donne les symbolisations de la porte ET et la table logique:

La porte logique OU

La porte OU a 2 bits en entrée et un seul bit de sortie.

• Si les 2 bits d’entrée valent \(0\), alors le bit de sortie vaut \(0\).

• Si un bit d’entrée ou les 2 valent \(1\), alors le bit de sortie vaut \(1\).

On donne les symbolisations de la porte OU et la table logique:

Algèbre de Boole

George Boole est un mathématicien britannique qui s’est intéressé à l’algèbre des opérateurs logiques.

Les 3 opérateurs logiques NOT, AND et OR sont appelés opérateurs booléens.

Les valeurs appliquées aux opérateurs sont les opérandes qui ont pour valeur True (1) ou False (0).

Le résultat d’une expression logique est donc soit True, soit False.

Opérateur NOT

L’opérateur NOT s’applique à un seul opérande \(x\) qui se note NOT(\(x\)) ou \(\neg(x)\).

table de vérité de NOT

A	NOT(A)
True	False
False	True

Opérateur AND

L’opérateur AND s’applique à deux opérandes \(x\) et \(y\) qui se note \(x\) AND \(y\) ou \(x \wedge y\).

table de vérité de AND

A	B	A AND B
False	False	False
False	True	False
True	False	False
True	True	True

Opérateur OR

L’opérateur OR s’applique à deux opérandes \(x\) et \(y\) qui se note \(x\) OR \(y\) ou \(x \vee y\).

table de vérité de OR

A	B	A OR B
False	False	False
False	True	True
True	False	True
True	True	True

Expression booléenne

Une expression booléenne est une expression constituée de valeurs booléennes (True ou False), d’opérateurs (NOT, AND, OR) et de parenthèses. Une expression booléenne se calcule et a pour valeur TRUE ou FALSE.

Ces expressions booléennes respectent des règles de priorité comme en mathématiques:

1. Les parties entre parenthèses sont d’abord évaluées;

2. L’opérateur NOT est le premier opérateur évalué;

3. L’opérateur AND est le second opérateur évalué;

4. L’opérateur OR est le dernier opérateur évalué.

Note

Pour éviter toute erreur, il est conseillé d’utiliser des parenthèses mêmes si elles sont superflues.

Exemple

Soit l’expression booléenne \(A\) AND (NOT(\(B\)) OR \(C\)). Pour évaluer cette expression, on écrit la table de vérité.

table de vérité de l’expression booléenne

A	B	C	NOT(B)	NOT(B) OR C	A AND (NOT(B) OR C)
False	False	False	True	True	False
False	False	True	True	True	False
False	True	False	False	False	False
False	True	True	False	True	False
True	False	False	True	True	True
True	False	True	True	True	True
True	True	False	False	False	False
True	True	True	False	True	True

Astuce

Si une expression booléenne contient \(N\) variables, la table de vérité contient \(2^{N}\) lignes.

Les tests

En programmation, les expressions booléennes sont très utilisées pour exécuter ou non des instructions. Dans une expression booléenne, les valeurs sont obtenues à partir de tests de comparaison. Les principaux opérateurs de comparaison sont l’opérateur égal, l’opérateur inférieur et l’opérateur supérieur.

Note

L’opérateur égal est noté par un double signe d’égalité: \(a\) == 5.

Exemple

Soit \(n\) un nombre entier positif non nul.

Pour quelles valeurs de ce nombre \(n\), l’expression booléenne NOT(n == 2) AND n < 4 est-elle vraie ?

En s’appuyant sur la table de vérité de l’opérateur AND, on sait que l’expression est vraie lorsque les 2 tests sont vrais en même temps.

Cette expression est vraie lorsque le nombre \(n\) vaut \(1\) ou \(3\).