Convertir des nombres entiers#
Écriture binaire à écriture décimale#
La conversion d’un nombre binaire en écriture décimale se fait en associant à chaque chiffre de l’écriture binaire la puissance de 2 qui correspond à sa position.
Le tableau ci-dessous redonne les 8 premières puissances de 2, soit pour 1 octet :
\(2^{7}\) |
\(2^{6}\) |
\(2^{5}\) |
\(2^{4}\) |
\(2^{3}\) |
\(2^{2}\) |
\(2^{1}\) |
\(2^{0}\) |
|---|---|---|---|---|---|---|---|
128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
Exemple
Le nombre binaire 1101 est associée aux puissances de 2 d’exposant 0, 2 et 3 (de gauche à droite).
Donc le nombre binaire 1101 s’écrit 13 en décimal.
Écriture décimale à écriture binaire#
La conversion d’un nombre entier décimal en écriture binaire se fait en décomposant ce nombre en une somme de puissance de 2, en commençant par la plus grande puissance possible.
Voici un algorithme présentant la méthode:
n désigne le nombre en écriture décimale
Tant que n non nul:
On soustrait la plus grande puissance de 2 au nombre n
On affecte la différence au nombre n.
On renvoie les différentes puissances de 2 utilisées
Exemple
On donne ci-dessous la conversion en binaire du nombre décimal 41:
- \(32=2^{5}\) est la plus grande puissance de 2 que l’on peut enlever à 41;
il reste \(41-32=9\).
- \(8=2^{3}\) est la plus grande puissance de 2 que l’on peut enlever à 9;
il reste alors \(9-8=1\).
- \(1=2^{0}\) est la plus grande puissance de 2 que l’on peut enlever à 1;
il reste alors \(1-1=0\).
Le nombre 41 s’écrit en binaire:
Astuce
Pour convertir un nombre entier décimal en binaire, on peut remplacer la soustraction par la division euclidienne. En voici l’algorithme:
n est le nombre décimal à convertir en binaire
Tant que n est non nul:
On divise n par 2.
On affecte à n le quotient entier obtenu
On renvoie les restes des divisions en partant du dernier calculé.
Ci-dessous les différentes divisions euclidiennes à calculer.
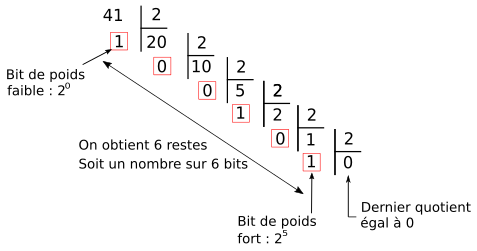
Comme pour la méthode précédente, on obtient \(41_{10}=101001_{2}\).
Écriture binaire à écriture hexadécimale#
La conversion d’un nombre binaire en écriture hexadécimale est beaucoup plus simple.
On regroupe les chiffres de l’écriture binaire par groupe de 4 bits appelé quartet, en commençant par la gauche. Ensuite on convertit chaque quartet en chiffre hexadécimal.
Exemple
Le nombre 1101001 est écrit sur 7 bits.
On le décompose en 2 quartets 110 et 1001. On ajoute le bit 0 au début du premier quartet sans que ça change sa valeur.
On convertit chaque quartet:
\(0110_{2}=6_{16}\)
\(1001_{2}=9_{16}\)
Le nombre binaire 1101001 s’écrit 69 en hexadécimal.
Écriture hexadécimale à écriture binaire#
La conversion en binaire d’un nombre hexadécimal est simple aussi.
Chaque chiffre hexadécimal est remplacé par son quartet en binaire.
Exemple
Le nombre \(A8_{16}\) a pour chiffres hexadécimaux A et 8.
Le chiffre A se convertit en binaire par 1010;
le chiffre 8 se convertit en binaire par 1000.
En associant ces deux quartets, on obtient l’écriture binaire : \(A8_{16} = 10101000_{2}\).
Écriture hexadecimale et à écriture décimale#
La conversion d’un nombre en écriture hexadécimale en écriture décimale se fait comme en binaire. Chaque chiffre de l’écriture hexadécimale est multiplié par la puissance de 16 à laquelle correspond sa position.
Le tableau ci-dessous redonne les 5 premières puissances de 16 :
\(16^{4}\) |
\(16^{3}\) |
\(16^{2}\) |
\(16^{1}\) |
\(16^{0}\) |
|---|---|---|---|---|
65536 |
4096 |
256 |
16 |
1 |
Exemple
Par exemple, le nombre \(A8_{16}\) se convertit en décimal en effectuant le calcul:
Le nombre hexadécimal \(A8_{16}\) a pour valeur décimale 168.
Écriture décimale à écriture hexadécimale#
La conversion d’un nombre décimal en hexadécimal est plus délicate. On peut utiliser les mêmes méthodes que pour la conversion en binaire, à savoir par soustraction de puissances de 16 ou les divisions euclidiennes par 16.
Exemple
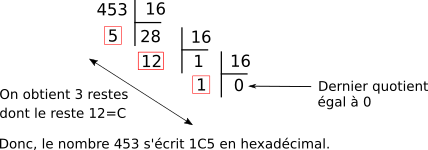
Le nombre entier positif 453 se convertit en hexadécimal par \(453_{10}=1C5_{16}\).
On donne les divisions successives de la conversion.
Astuce
Pour convertir un nombre hexadécimal en décimal et inversement, il est parfois plus simple de passer par l’écriture binaire.