Les arbres binaires

Les structures arborescentes ou plus simplement arbres sont des structures de données hiérarchiques.

On peut définir un arbre par sa description hiérarchique :

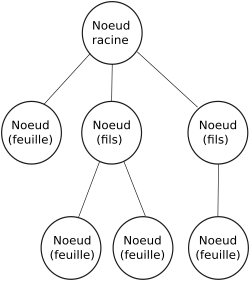
• Au départ, on a un noeud racine qui possède plusieurs noeuds fils. Le noeud racine est alors le père des noeuds fils.

• Les fils sont reliés au noeud père par des arêtes ou des branches. Les noeuds fils ont eux-mêmes des noeuds fils.

• Si un noeud n’a pas de fils, alors c’est une feuille.

Arbre binaire

Définition

Un arbre binaire est un arbre dont chaque nœud a au plus deux fils.

On peut définir récursivement un arbre binaire:

• soit c’est un nœud sans fils (feuille) éventuellement vide;

• soit c’est un nœud racine qui a deux fils: un fils gauche et un fils droit qui sont eux-mêmes des arbres binaires.

La figure suivante est un arbre binaire. Chaque noeud qui n’est pas une feuille possède au moins un sous-arbre binaire.

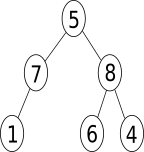
• Le nœud racine contient la valeur entière 5.

• Le noeud racine a 2 sous-arbres : un sous-arbre binaire gauche qui a une racine de valeur 7 et un sous-arbre binaire droit qui a une racine de valeur 8.

• L’arbre binaire possède 3 feuilles qui ont les valeurs 1, 6 et 4.

Définitions

1. Taille : nombre de noeuds (intermédiaires et feuilles) que possède un arbre.

2. Profondeur : la profondeur d’un noeud correspond à sa position dans l’arbre. La valeur attribuée à la profondeur d’un noeud dépend de la profondeur attribuée à la racine.

   • Soit la racine est de profondeur 0 et cela signifie que la profondeur d’un nœud correspond au nombre de branches le séparant de la racine.

   • Soit la racine est de profondeur 1 et cela signifie que la profondeur d’un nœud correspond au nombre de noeuds jusqu’à la racine.

3. Niveau : tous les noeuds d’un arbre qui ont la même profondeur p.

4. Hauteur : profondeur maximale d’un noeud de l’arbre.

On reprend l’arbre binaire précédent en posant la profondeur du noeud racine égale à 0.

• L’arbre possède 6 noeuds donc sa taille est 6.

• Le noeud contenant la valeur 6 a une profondeur de 2. Il y a 2 arêtes entre la racine et ce nœud.

• Le niveau 2 contient les noeuds de valeur 1, 6 et 4; ce sont des feuilles.

• La hauteur de cet arbre est égale à 2, ce qui correspond à la plus grande profondeur, celle des feuilles.

Avertissement

On convient que la racine est de profondeur \(0\) et donc de hauteur \(0\). Si la racine a une hauteur de 0, alors un arbre vide a une hauteur de -1.

Arbres binaires particuliers

Les arbres binaires peuvent avoir des formes très différentes. Deux arbres binaires qui ont la même hauteur n’ont pas nécessairement le même nombre de noeuds. Certains arbres ont très peu de noeuds alors que d’autres en ont beaucoup. On distingue ci-après plusieurs formes d’arbres binaires.

Arbre filiforme

Définition

Un arbre binaire est filiforme si chaque noeud a exactement 1 fils.

Propriété

Un arbre binaire filiforme de hauteur h vérifie :

• Chaque niveau de profondeur p contient 1 noeud.

• L’arbre a une taille n=h+1 noeuds.

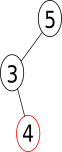
L’arbre donné ci-dessous est filiforme de hauteur h=2. On voit que chaque noeud a un seul fils, à droite ou à gauche. La taille de cet arbre est n=3.

Arbre binaire complet

Définition

Un arbre binaire est complet si chaque noeud a exactement 2 fils. C’est un arbre binaire sans trous.

Propriété

Un arbre binaire complet de hauteur h vérifie:

• Chaque niveau de profondeur p contient \(2^{p}\) noeuds.

• L’arbre a une taille \(n=2^{h+1}-1\) noeuds.

L’arbre binaire représenté ci-dessous est complet. Chaque noeud qui n’est pas une feuille a exactement 2 sous-arbres gauche et droit.

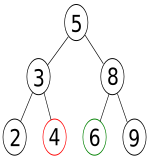
L’arbre est complet de hauteur h=2.

• Le niveau de profondeur p=1 contient \(2^{1}=2\) noeuds.

• La taille de cet arbre est \(n=2^{3}-1=7\) noeuds.

Arbre binaire tassé

Définition

Un arbre binaire est bien tassé si chaque noeud a exactement 2 fils sauf sur le dernier niveau où il manque des feuilles, celles situées le plus à droite.

Propriété

Un arbre binaire bien tassé de hauteur h vérifie:

• Chaque niveau de profondeur p contient \(2^{p}\) noeuds, sauf le dernier niveau (les feuilles) qui en contient au plus \(2^{h}\).

• L’arbre a une taille n comprise entre la taille d’un arbre complet de hauteur h-1 et la taille d’un arbre complet de hauteur h: \(2^{h}-1 \leqslant n \leqslant 2^{h+1}-1\).

L’arbre binaire sur la figure ci-dessous est bien tassé de hauteur h=2.

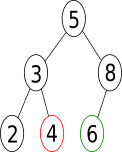
La taille n de cet arbre est comprise entre la taille d’un arbre complet de hauteur h-1 et la taille d’un arbre complet de hauteur h, donc ici :

\[2^{2}-1 \leqslant n \leqslant 2^{3}-1 \Longleftrightarrow 3 \leqslant n \leqslant 7.\]

Ici, on vérifie que l’arbre bien tassé a une taille \(n=6\) noeuds comprise entre 3 et 7.

Taille et hauteur d’un arbre binaire

On suppose que la racine de l’arbre est de profondeur 0.

Arbre de hauteur connue

Propriété

Un arbre de hauteur h a une taille n telle que: \(\boxed{h+1 \leqslant n \leqslant 2^{h+1}-1}\)

• Au minimum, l’arbre est filiforme donc a un seul noeud à chaque niveau et alors n=h+1 noeuds pour être de hauteur h;

• Au maximum, si l’arbre est complet, on a \(2^{p}\) noeuds à chaque niveau p et donc \(2^{h}\) noeuds sur le niveau de profondeur h.

Indication

Le nombre de noeuds à chaque niveau est le terme d’une suite géométrique de raison \(2\) dont la somme de tous les termes vaut \(2^{h+1}-1\).

Arbre de taille connue

Propriété

Un arbre de taille n fixée a une hauteur h qui vérifie \(\boxed{\log_{2}(n) \leqslant h \leqslant n-1}\).

• Au maximum, l’arbre est filiforme de n nœuds a une hauteur h=n-1;

• Au minimum, si l’arbre est bien tassé alors le nombre de nœuds n est compris entre \(2^{h}-1\) et \(2^{h+1}-1\).

Un arbre a une taille n=17. Selon la forme de cet arbre, sa hauteur varie.

• Le nombre \(17\) est encadré par les puissances de 2 : \(2^{4}=16\) et \(2^{5}=32\) donc \(\log_{2}(17)\) est compris entre 4 et 5, ce qui permet d’affirmer que la hauteur h est supérieure à 4.

• La hauteur h est inférieure ou égale à n-1=17-1=16.

Conclusion : la hauteur \(h\) d’un arbre de taille \(n=17\) est comprise entre \(4\) et \(16\).