Ctrl+K

Epreuve pratique

Epreuve pratique#

Sujet 03 - Exercice 2#

Une expression arithmétique ne comportant que les quatre opérations +, -, x, ÷ peut être représentée sous forme d’arbre binaire. Les noeuds internes sont des opérateurs et les feuilles sont des nombres. Dans un tel arbre, la disposition des noeuds joue le rôle des parenthèses que nous connaissons bien.

En parcourant en profondeur infixe l’arbre binaire ci-dessous, on retrouve l’expression notée habituellement :

\[3 \times (8 + 7) - (2 + 1)\]
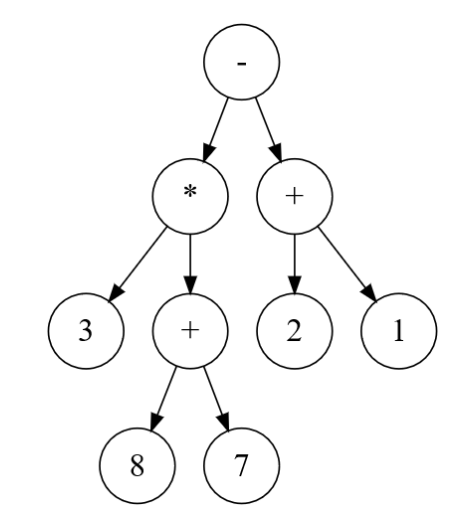
../_images/ep_03.png

La classe Noeud ci-après permet d’implémenter une structure d’arbre binaire.

Compléter la fonction récursive expression_infixe qui prend en paramètre un objet de la classe Noeud et qui renvoie l’expression arithmétique représentée par l’arbre binaire passé en paramètre, sous forme d’une chaîne de caractères contenant des parenthèses.

Résultat attendu avec l’arbre ci-dessus :

>>> e = Noeud(Noeud(Noeud(None, 3, None), '*', Noeud(Noeud(None, 8, None), '+', Noeud(None, 7, None))), '-', Noeud(Noeud(None, 2, None), '+', Noeud(None, 1, None)))

>>> expression_infixe(e)
'((3*(8+7))-(2+1))'

class Noeud:
    """
    Classe implémentant un noeud d'arbre binaire disposant de 3 attributs:
    - valeur : la valeur de l'étiquette,
    - gauche : le sous-arbre gauche,
    - droit : le sous-arbre droit.
    """
    def __init__(self, g, v, d):
        self.gauche = g
        self.valeur = v
        self.droit = d
    
    def __str__(self):
        return "Noeud(" + str(self.gauche) + ',' + str(self.valeur) + ',' + str(self.droit) + ")"
    
    def est_une_feuille(self):
        '''Renvoie True si et seulement si le noeud est une feuille'''
        return self.gauche is None and self.droit is None


def expression_infixe(e):
    s = ...
    if e.gauche is not None:
        s = s + expression_infixe(...)
    s = s + ...
    if ... is not None:
        s = s + ...
    if ...:
        return s
    
    return '('+ s +')'

Sujet 27 - Exercice 1#

Dans cet exercice, un arbre binaire de caractères est stocké sous la forme d’un dictionnaire où les clefs sont les caractères des noeuds de l’arbre et les valeurs, pour chaque clef, la liste des caractères des fils gauche et droit du noeud.

Par exemple, l’arbre

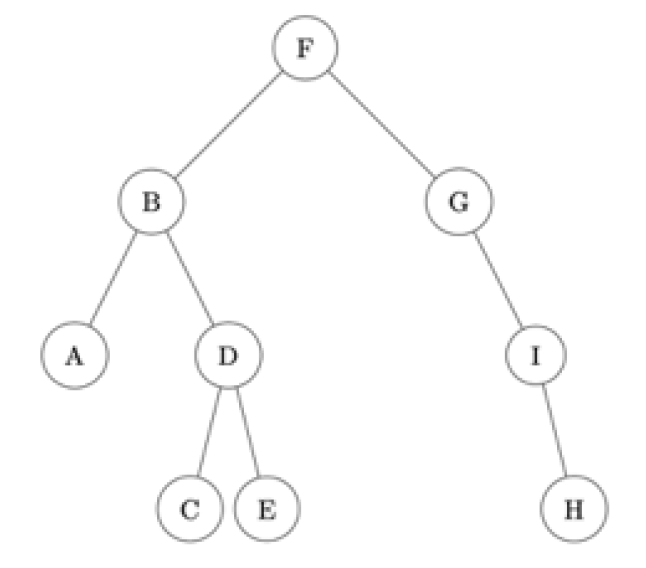
../_images/ep_27.png

est stocké dans:

>>> a = {'F':['B','G'], 'B':['A','D'], 'A':['',''], 'D':['C','E'], 'C':['',''], 'E':['',''], 'G':['','I'], 'I':['','H'], 'H':['','']}

Écrire une fonction récursive taille prenant en paramètres un arbre binaire arbre sous la forme d’un dictionnaire et un caractère lettre qui est la valeur du sommet de l’arbre, et qui renvoie la taille de l’arbre à savoir le nombre total de noeud.

On pourra distinguer les 4 cas où les deux « fils » du noeud sont '', le fils gauche seulement est '', le fils droit seulement est '', aucun des deux fils n’est ''.

Exemple :

>>> taille(a,'F')
9
Contenu