Ctrl+K

Activité découverte : ABR

Activité découverte : ABR#

Un arbre binaire de recherche (ABR) est un arbre binaire dont les noeuds contiennent des clés (valeurs) que l’on peut comparer comme des nombres entiers ou les lettres de l’alphabet.

Un ABR respecte les règles suivantes:

  1. Pour un noeud donné:

    • Toutes les clés situées dans l’arbre fils gauche sont inférieures à la clé du noeud ;

    • Toutes les clés situées dans l’arbre fils droit sont supérieures à la clé du noeud ;

  2. Toutes les clés d’un ABR sont distinctes, pas de doublon.

Partie 1#

  1. Les arbres ci-dessous sont-ils des arbres binaires de recherche (ABR) ? Justifier votre réponse.

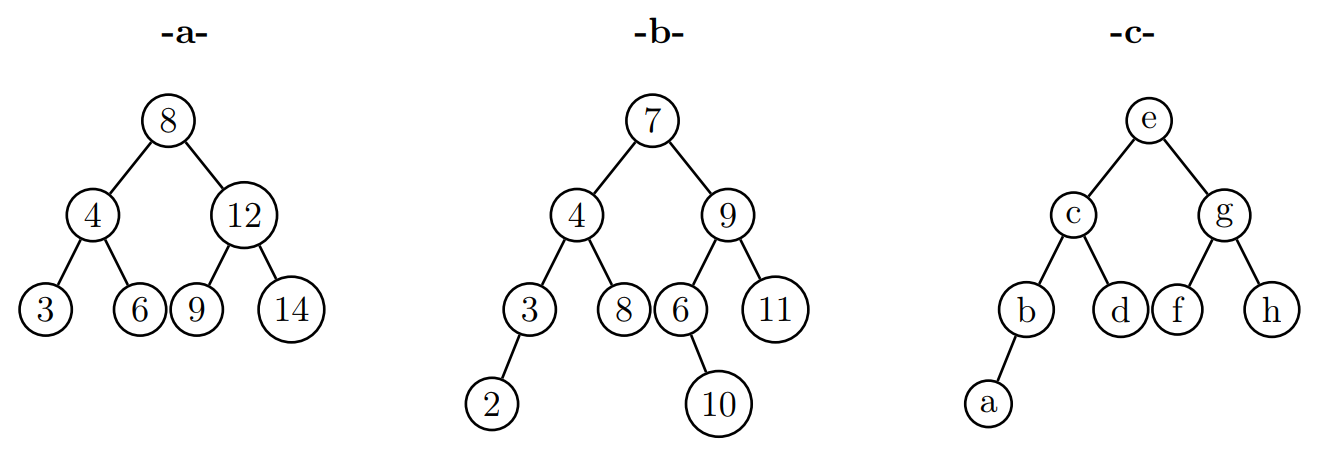
    ../_images/activite_fig1.png

  2. Un arbre binaire de recherche contient les nombres entiers de 1 à 10. Représenter dans chacun des cas suivants cet arbre binaire sachant que la racine est de hauteur 0 et que:

    1. la racine de l’arbre est le nombre 5 et sa hauteur est minimale.

    2. la racine de l’arbre est le nombre 3 et sa hauteur est 3.

    3. la racine de l’arbre est le nombre 9 et la hauteur est maximale.

Partie 2#

On reprend l’implémentation des arbres binaires en POO. On dispose de deux classes pour implémenter les ABR: la classe Arbre et la classe Noeud.

  • Tout objet créé avec la classe Arbre a un attribut racine.

    • L’attribut racine initialisé à None définit un arbre vide;

    • Pour un arbre non vide, la racine prend la valeur d’un objet Noeud .

    Nous avons les méthodes des arbres binaires:

    • La méthode est_vide() renvoie le booléen True pour un arbre vide et False pour un arbre non vide.

    • La méthode fils_gauche() renvoie l’arbre gauche d’un Noeud.

    • La méthode fils_droit() renvoie l’arbre droit d’un Noeud.

  • La classe Noeud contient 3 attributs : valeur, gauche et droit.

    • L’attribut valeur contient la valeur d’un noeud de l’arbre;

    • Les attributs gauche et droit représentent des arbres binaires qui sont des objets Noeud éventuellement vides.

    Elle ne contient pas de méthode particulière en dehors de l’affichage.

  1. Soit \(a\) un ABR tel que a=(5, (3, None, None), (6, None, None)).

    1. Représenter schématiquement l’ABR a.

    2. On ajoute dans cet ABR le noeud de valeur \(4\). Compléter la description récursive de a.

  2. On définit avec l’implémentation EN POO notre ABR en python.

    1. Quelle instruction Python construit l’arbre a ?

    2. Soit b = a.fils_gauche() ? Quel est le type de la variable b ?

    3. Que renvoie b.est_vide() ?

    4. Ajouter la valeur \(4\) dans l’arbre a.

Partie 3#

Dans cette partie, nous allons créer deux fonctions pour rechercher et insérer une valeur dans un ABR.

  1. La recherche d’une valeur dans un ABR nécessite de parcourir l’arbre jusqu’à trouver la valeur si elle est présente. Le parcours d’un arbre est récursif, donc la recherche d’une valeur s’appuie sur la récursivité.

    On donne ci-après l’algorithme de recherche d’une valeur x dans un arbre:

    si arbre vide:
    valeur de x non présente
sinon:
    si x < valeur du Noeud visité:
        on renvoie la recherche de x dans l'arbre gauche
    sinon si x > valeur Noeud visité:
        on renvoie la recherche de x dans l'arbre droit
    sinon:
        valeur de x présente

    a. Écrire la fonction appartient qui prend en paramètre la valeur \(x\) cherchée et un arbre binaire de recherche. Cette fonction est de type booléen, elle renvoie True si la valeur est dans l’arbre, False sinon.

    1. Vérifier votre fonction et votre méthode avec l’arbre a créé dans la première partie.

  2. L’ajout d’une valeur dans un ABR nécessite aussi le parcours récursif de l’arbre et l’ajout d’un Noeud .

    On donne ci-après l’algorithme de l’ajout d’une valeur x dans un arbre a.

    si arbre a est vide:
    a = Arbre(x)
sinon:
    si x < valeur du noeud visité:
        si le noeud gauche vide:
            noeud gauche = Noeud(x)
        sinon:
            on ajoute x dans arbre gauche
    si x > valeur noeud visité:
        si le droit vide:
            noeud droit = Noeud(x)
        sinon:
            on ajoute x dans arbre droit
renvoi de arbre a

    1. Écrire la fonction ajoute qui prend en paramètre la valeur x à ajouter et un arbre binaire de recherche. Elle renvoie un arbre binaire avec la valeur ajoutée.

    2. Vérifier votre fonction avec l’arbre a créé dans la première partie en y ajoutant différentes valeurs.

Contenu