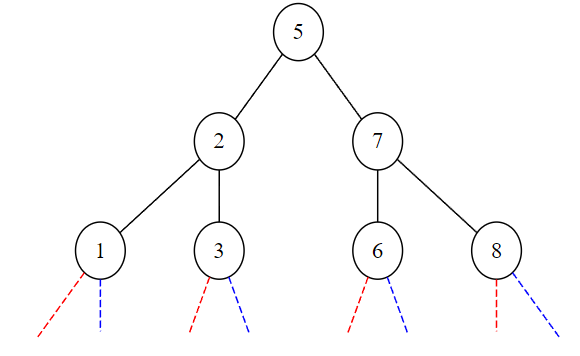
Arbre binaire de recherche (ABR)#
Définition
Un arbre binaire de recherche est un arbre binaire tel que pour un noeud fixé de l’arbre, tout noeud de son arbre fils gauche lui est strictement inférieur et tout noeud de son arbre fils droit lui est strictement supérieur.
Les valeurs d’un ABR sont appelées des clés. Les clés sont distinctes, l’arbre ne possède aucun doublon.
Prudence
Un même ensemble de données peut être représenté par différents arbres binaires de recherche. Certains ABR auront une structure proche d’un arbre binaire complet ou bien tassé. On dit que ces ABR sont équilibrés.
Prenons l’exemple d’un arbre binaire de recherche (ABR) donné ci-dessous.
La racine de l’arbre a pour clé \(5\);
L’arbre fils gauche contient les clés \(2\), \(3\) et \(4\) inférieures à \(5\);
L’arbre fils droit contient les clés \(6\), \(8\) et \(9\) supérieures à \(5\).
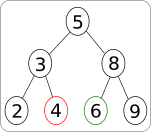
Le noeud de valeur
4se situe dans l’arbre fils gauche du noeud de clé égale à5puisque \(4 < 5\); Il est dans l’arbre fils droit du noeud de clé égale à3puisque \(4 > 3\).Le noeud de valeur
6se situe dans l’arbre fils droit de la racine de clé5puisque \(6 > 5\); Il est dans un arbre fils gauche du noeud de clé égale à8puisque \(6 < 8\).L’arbre binaire est équilibré. D’autres ABR peuvent être construits avec les mêmes données comme le montre les figures ci-dessous.
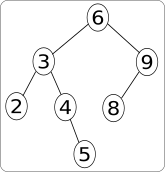
arbre déséquilibré à gauche#
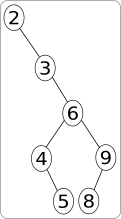
arbre déséquilibré à droite#
Implémentation en Python#
L’implémentation d’un arbre binaire peut se faire avec des listes, dictionnaires ou par programmation objet.
Le choix de la programmation objet pour implémenter nos ABR reprend celle mise en place pour les arbres binaires.
La classe Noeud instancie un objet Noeud avec 3 attributs:
valeur,gauche,droit;La classe Arbre instancie un objet Arbre avec un seul attribut :
racine. La racine est un objet Noeud éventuellement vide.
Le code python de cette implémentation est le suivant:
class Noeud:
def __init__(self, valeur, gauche=None, droit=None):
# instancie, crée un objet Noeud avec ces trois attributs
self.valeur = valeur
self.gauche = gauche
self.droit = droit
def __str__(self):
# crée une chaine de caratères pour afficher un objet Noeud avec la commande print
if self.valeur is None:
return ""
else:
return "Noeud("+str(self.valeur) + ","+ str(self.gauche) +","+ str(self.droit)+")"
class Arbre:
def __init__(self,racine=None):
# instancie, crée un objet Arbre avec un seul attribut dont la valeur est un objet Noeud.
if isinstance(racine,Noeud):
self.racine = racine
else:
self.racine = Noeud(racine)
def __str__(self):
# appelle la méthode de l'objet Noeud pour être affiché
return str(self.racine)
def est_vide(self):
# teste si l'arbre est vide
return self.racine.valeur is None
def fils_gauche(self):
# renvoie le contenu d'un noeud fils gauche en arbre
return Arbre(self.racine.gauche)
def fils_droit(self):
# renvoie le contenu d'un noeud fils droit en arbre
return Arbre(self.racine.droit)
On se propose de créer l’arbre binaire de recherche, équilibré, de la première figure.
On crée les feuilles de l’ABR:
>>> n_2 = Noeud(2)
>>> n_4 = Noeud(4)
>>> n_6 = Noeud(6)
>>> n_9 = Noeud(9)
On crée le noeud gauche; sa racine a pour valeur 3, à sa gauche c’est le noeud n_2 et sa droite le noeud n_4:
>>> n_g = Noeud(3,n_2,n_4)
On crée le noeud droit; sa racine a pour valeur 8, à sa gauche c’est le noeud n_6 et à sa droite le noeud n_9:
>>> n_d = Noeud(8,n_6,n_9)
On crée le noeud qui contient tous les autres noeuds:
>>> n = Noeud(5,n_g,n_d)
On crée notre objet Arbre dont l’attribut racine a pour valeur le noeud n:
>>> a= Arbre(n)
>>> print(a)
On obtient l’arbre binaire de recherche suivant:
Noeud(5, Noeud(3, Noeud(2, None, None), Noeud(4, None, None)), Noeud(8, Noeud(6, None, None), Noeud(9, None, None)))
Recherche d’une clé dans un ABR#
Un arbre binaire de recherche est soit vide, soit constitué d’un noeud racine et de 2 arbres binaires de recherche gauche et droit éventuellement vides.
La recherche d’une clé (valeur) dans un ABR s’appuie sur le parcours récursif de l’arbre. On en donne l’algorithme ci-dessous:
Algorithme
- si arbre vide:
valeur x non présente
- sinon:
- si x < valeur du Noeud visité:
on recherche la valeur x dans l’arbre gauche (appel récursif)
- sinon si x > valeur Noeud visité:
on recherche la valeur x dans l’arbre droit (appel récursif)
- sinon:
la valeur x est trouvée
Avec l’implémentation en python des ABR, cet algorithme s’écrit avec une fonction récursive:
def recherche(x,a):
if a.est_vide():
return False
else:
if x < a.racine.valeur:
return recherche(x,a.fils_gauche())
elif x > a.racine.valeur:
return recherche(x,a.fils_droit())
else:
return True
Ajouter une clé dans un ABR#
On donne ci-après le processus pour ajouter une clé (valeur) dans un ABR:
Si l’arbre est vide, on crée un Noeud avec la valeur à ajouter et on l’affecte à la racine de l’arbre;
Sinon, on parcourt récursivement l’arbre jusqu’à la bonne position et on ajoute un Noeud avec la valeur donnée.
En suivant ce processus, l’algorithme s’écrit:
Algorithme
- si arbre a est vide:
a.racine = Noeud(x)
- sinon:
- si x < valeur du noeud visité:
- si le noeud gauche est vide:
on ajoute un noeud gauche avec la valeur x
- sinon:
on ajoute x dans arbre gauche (appel récursif)
- si x > valeur noeud visité:
- si le noeud droit est vide:
on ajoute un noeud droit avec la valeur x
- sinon:
on ajoute x dans arbre droit (appel récursif)
Avec l’implémentation en POO de notre ABR:
def inserer(x,a):
if a.est_vide():
a.racine = Noeud(x)
else:
if x < a.racine.valeur:
if a.racine.gauche is None:
a.racine.gauche = Noeud(x)
else:
inserer(x,a.fils_gauche())
if x > a.racine.valeur:
if a.racine.droit is None:
a.racine.droit = Noeud(x)
else:
inserer(x,a.fils_droit())
return a
Cette fonction insère des valeurs dans un ABR, y compris lorsque celui-ci est vide. En conséquence, cette fonction permet de créer des ABR et de les compléter facilement sans avoir à créer chaque Noeud.
On crée un ABR avec la classe Arbre:
>>> a = Arbre()
>>> print("a est un arbre vide:",a.racine)
a2 est un arbre vide:
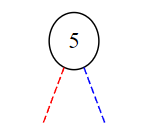
On ajoute la clé de valeur 5 à la racine de l’arbre avec la fonction inserer.
>>> a = inserer(5,a)
>>> print("a possède un noeud de clé 5:",a.racine.valeur)
a possède un noeud de clé 5: Noeud(5,None,None)
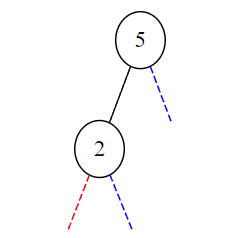
On insère la clé de valeur 2 dans l’arbre. Elle se place dans le sous-arbre gauche de la racine.
>>> a = inserer(2,a)
>>> print(a)
Noeud(5,Noeud(2,None,None),None)
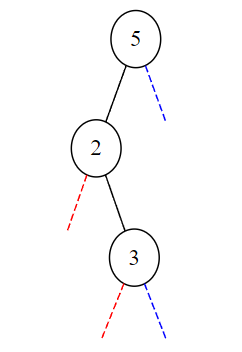
On insère ensuite la clé de valeur 3.
>>> a = inserer(3,a)
>>> print(a)
Noeud(5,Noeud(2,None,Noeud(3,None,None)),None)
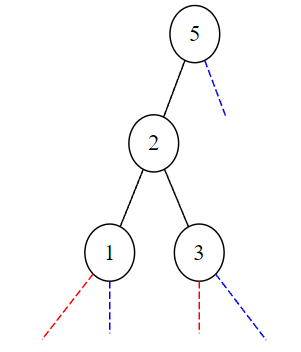
On insère la clé de valeur 1.
>>> a = inserer(1,a)
>>> print(a)
Noeud(5,Noeud(2,Noeud(1,None,None),Noeud(3,None,None)),None)
On insère la clé de valeur 7. Cette clé est supérieure à la clé de la racine, donc elle est insérée dans le sous-arbre droit de la racine.
>>> a2 = inserer(7,a2)
>>> print(a)
Noeud(5,Noeud(2,Noeud(1,None,None),Noeud(3,None,None)),Noeud(7,None,None))
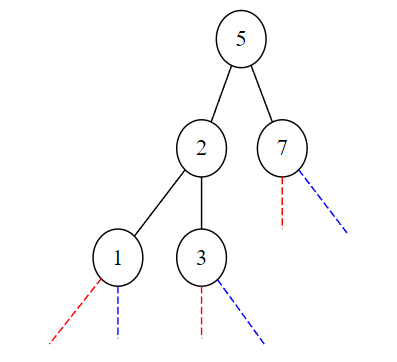
On insère la clé de valeur 6.
>>> a = inserer(6,a)
>>> print(a)
Noeud(5,Noeud(2,Noeud(1,None,None),Noeud(3,None,None)),Noeud(7,Noeud(6,None,None),None))
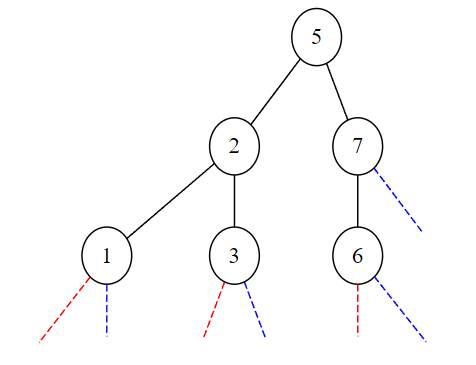
On insère la clé de valeur 8.
>>> a = inserer(8,a)
>>> print(a)
Noeud(5,Noeud(2,Noeud(1,None,None),Noeud(3,None,None)),Noeud(7,Noeud(6,None,None),Noeud(8,None,None)))