Exercices

Exercice 1

1. Donner tous les ABR de taille 3 contenant les nombres entiers \(1\), \(2\) et \(3\).

2. On ajoute dans un ABR vide les nombres \(5\), \(6\), \(2\), \(4\), \(1\) et \(3\) dans cet ordre. Quel est l’ABR obtenu?

3. Construire un ABR de hauteur 3 (racine de hauteur 1) contenant les nombres entiers \(1\), \(2\), etc. et qui est complet.

4. Créer un ABR complet contenant les nombres entiers de \(1\) à \(15\).

5. Donner un ABR bien tassé comprenant les nombres entiers de \(1\) à \(11\).

Exercice 2

1. Soit \(L\) la liste python telle que : L = [25,19,32,13,24,27,33,21,29].

   On parcourt la liste du premier élément au dernier en les ajoutant dans un ABR initialement vide. Représenter cet ABR une fois complété.

2. On donne l’ABR ci-dessous:

   

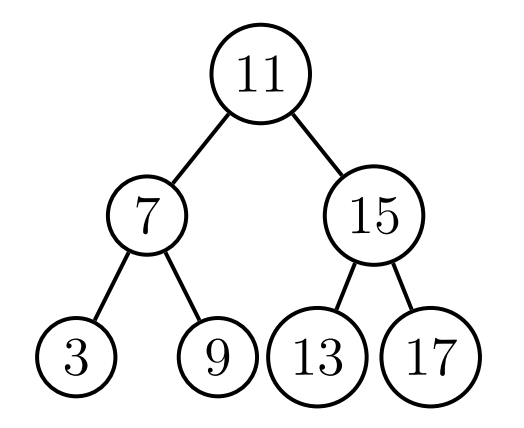
   Quelle liste de nombres permet de construire cet ABR en la parcourant du premier au dernier élément ?

3. Comment parcourir un ABR pour avoir ses valeurs rangées par ordre croissant ? Écrire une fonction de parcours qui renvoie une liste triée des valeurs contenues dans l’ABR.

4. On souhaite créer deux fonctions qui transforment une liste en ABR et réciproquement.

   1. Écrire une fonction en Python, liste_en_abr qui prend en paramètre une liste de nombres et renvoie un ABR contenant les valeurs de la liste. Les valeurs de l’ABR sont ajoutées en suivant l’ordre de la liste, c’est à dire du premier au dernier élément.

   2. Quel parcours d’arbre binaire faut-il utiliser pour obtenir les valeurs dans le même ordre que la liste qui a permis de le construire ?

      Écrire une fonction de parcours d’arbre qui renvoie la liste ayant permis de le construire.